Question

The unemployment rate in a city is 14%. If 8 people from the city are sampled at random, find the probability that fewer than 3 of them are unemployed.Carry your intermediate computations to at least four decimal places, and round your answer to two decimal places.

Answer 1

0.91

Explanation:

Given:

The probability that people are unemployed = 14% = 0.14

Therefore:

The probability that people are employed = 1 - 14% = 86% = 0.86

We can determine the desired probability with a binomial probability (p = 0.14, q = 0.86 and n = 8) when x = 0, 1 and 2.

Therefore:

`\begin{gathered} P(x<3)=P(x=0)+P(x=1)+P(x=2) \\ \\ P(x=0)=_8C_0\cdot(0.14)^0\cdot(0.86)^(8-0)=(8!)/(0!(8-0)!)\cdot(0.14)^0\cdot(0.86)^8=0.2992 \\ \\ P(x=1)=_8C_1\cdot(0.14)^1\cdot(0.86)^(7-1)=(8!)/(1!(8-1)!)\cdot(0.14)^1\cdot(0.86)^7=0.3897 \\ \\ P(x=2)=_8C_2\cdot(0.14)^2\cdot(0.86)^(8-2)=(8!)/(2!(8-2)!)\cdot(0.14)^2\cdot(0.86)^6=0.2220 \\ \\ P(x<3)=0.2992+0.3897+0.2220 \\ \\ P(x<3)=0.9109\cong0.91 \end{gathered}`

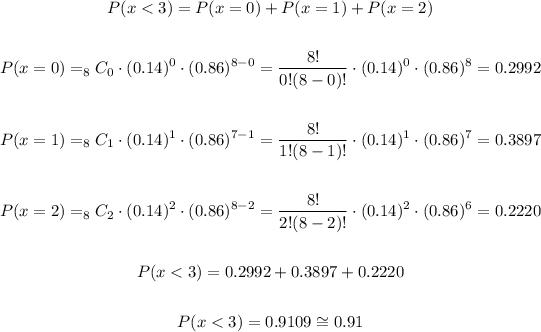
Therefore, the probability is equal to 0.91