Given:
A line passing through the points (4,5) and (2,-6).
The objective is to find the equation of line in slope-intercept form.
Step-by-step explanation:
Consider the given points as
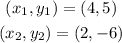
The slope of the line can be calculated as,

To find slope m:
On plugging the gven vales in rquation of slope,
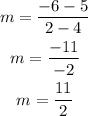
The general equation of straight line is,
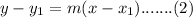
To find equation:
On plugging the values in the above equation.
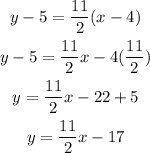
Hence, the equation of straight linne is y = (11/2)x - 17.
So the answer is correct.