Question

A certain strain of bugs had a population of 72. Two weeks later the population had reduced to 28.a) Develop the function of the form p = ae^kt that represents the population after t weeks.b) Use the function to predict when the population will be less than 1 bug (i.e. disappear).

Answer 1

(a)

`p=72\cdot e^(-0.472t)`

(b)

During the 9th week, in week 10, the population has already disappeared

Explanation:

We have that the function has the following form:

`p=a\cdot e^(kt)`

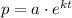
(a)

We can calculate the value of k, knowing that after two weeks the population dropped from 72 to 28, therefore we replace these values and solve for k, like this:

`\begin{gathered} 28=72\cdot e^(k\cdot2) \\ e^(2k)=(28)/(72) \\ 2k=\ln ((28)/(72)) \\ k=(\ln((28)/(72)))/(2) \\ k=-0.472 \end{gathered}`

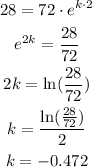
Therefore, the function would be:

`p=72\cdot e^(-0.472t)`

(b)

In order to predict when the population is less than 1, we must do the following inequality:

`\begin{gathered} 1<\: 72\cdot\: e^(-0.472t) \\ (1)/(72)(1)/(72) \\ -0.472t>\ln ((1)/(72)) \\ t<(\ln ((1)/(72)))/(-0.472) \\ t<9.05 \end{gathered}`

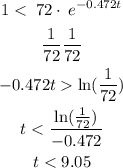
Which means that between the first 8 weeks the population will be greater than 1 and during the ninth week the population will begin to be less than 1