Question

If 100. g of gold-198 decays to 6.25g in 25.3 days, what is the half-life of gold-198?

Answer 1

Given

`\begin{gathered} N_0=100\text{ g} \\ t=25.3\text{ days} \\ N(t)=6.25\text{ g} \end{gathered}`

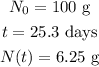
According to law of radioactive decay,

`N(t)=N_0e^(-\lambda t)`

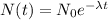
Rearranging equation in order to get rate constant,

`\lambda=(1)/(t)\ln ((N_0)/(N(t)))`

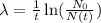
Substituting all known values,

`\begin{gathered} \lambda=\frac{1}{25.3\text{ days}}\ln (\frac{100\text{ g}}{6.25\text{ g}}) \\ =\frac{1}{25.3\text{ days}}\ln (16) \\ =0.109day^(-1) \end{gathered}`

The relation between the rate constant and the half life is given as,

`\begin{gathered} \text{half life=}(0.693)/(\lambda) \\ =(0.693)/(0.109day^(-1)) \\ =6.357\text{ days} \end{gathered}`

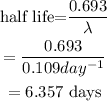
Therefore, half life of the Gold -198 is about 6.375 days.