Question

intravenous infusion are often made under gravity. The fluid is to flow through a tube from a raised bottle to a needle inserted in the vein. if the blood pressure is 80mm-Hg above atmospheric pressure, how high should the bottle be placed so that the fluid just enters the vein,assuming the fluid has a density of 1.5g/cm3

Answer 1

We know that the change in pressure is related to the change in height by:

`\Delta P=\rho g\Delta h`

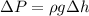
Let's assume that the vein is at the origin, then the change in height in this case would be the height of the bottle. Solving the equation above for the change in height we have:

`\Delta h=(\Delta P)/(\rho g)`

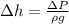
Now, before we plug any of the values we have to put them in the correct units; the pressure has to be in pascals, the density has to be in kg by cubic meters. We know that one mm-Hg is the same as 133.322 Pascals, then the pressure is:

`80(133.322)=10665.76`

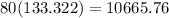
Now we change the density:

Now we plug the values in the equation above:

`\Delta h=(10665.76)/((1500)(9.8))=0.73`

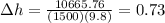
Therefore the height of the bottle is 0.73 meters (rounded to two decimal places)