Question

Amy is 7 Years older than jonny. Six years ago she was twice as old as he. How old is each now

Answer 1

To answer this question, we can proceed as follows:

1. Let x be Amy's age.

2. Let y be Jonny's age.

Six years ago, we have that the ages were:

A ---> x - 6

J ---> y - 6

And we have that six years ago, Amy was twice as old Jonny. Then, we have:

`(x-6)=2(y-6)`

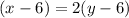
Currently, Amy is 7 years older than Jonny:

`x=y+7`

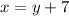
Now we have the next equations:

`(x-6)=2(y-6)`

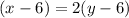
And

`x=y+7`

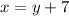
Expanding the first equation:

`(x-6)=2(y-6)\Rightarrow x-6=2y-12\Rightarrow x-2y=-12+6`

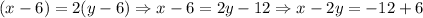
Then, we have:

`x-2y=-6`

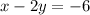
And the other equation can be rewritten as:

`x=y+7\Rightarrow x-y=7`

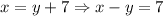
Then, we have the following system of equations:

`\begin{cases}x-2y=-6 \\ x-y=7\end{cases}`

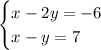
Now, to solve this system, we can multiply the first equation by -1, and then add both resulting equations as follows:

`\frac{\begin{cases}-1(x-2y=-6)=-x+2y=6 \\ x-y=7\Rightarrow x-y=7\end{cases}}{}`
`\frac{\begin{cases}-x+2y=6 \\ x-y=7\end{cases}}{y=13}`

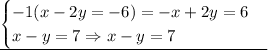
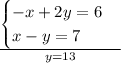
Then, we have that Jonny's age is 13 years old. Therefore, Amy's age is:

`x=y+7\Rightarrow x=13+7\Rightarrow x=20`

Then, Amy is 20 years old, and Jonny is 13 years old.

We can check the result using the age of both of them six years ago:

Amy ---> 20 - 6 = 14

Jonny ---> 13 - 6 = 7

As we can see, 6 years ago Amy was twice as old as Jonny.

In summary, we have that Amy's age is 20 years old and Jonny is 13 years old.