Answer:
a) The 90% confidence interval on the proportion of such graduates planning to continue their education is (0.2097, 0.2737).
b) The 95% confidence interval on the proportion of such graduates planning to continue their education is (0.2036, 0.2798).
c) Due to higher value of z, a 95% confidence interval, as in part b, is wider than a 90% confidence interval, found in part a, and is the difference between these two intervals.
d) Yes, because 0.25 is inside both intervals.
Explanation:
Question a:
In a sample with a number n of people surveyed with a probability of a success of
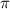 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
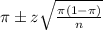
In which
z is the zscore that has a pvalue of
 .
.
117 of 484 new engineering graduates were planning to continue studying for an advanced degree.
This means that
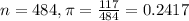
90% confidence level
So
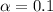 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
 , so
, so
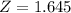 .
.
The lower limit of this interval is:
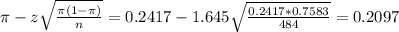
The upper limit of this interval is:
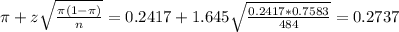
The 90% confidence interval on the proportion of such graduates planning to continue their education is (0.2097, 0.2737).
Question b:
95% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
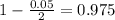 , so
, so
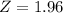 .
.
The lower limit of this interval is:
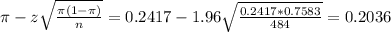
The upper limit of this interval is:
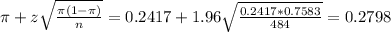
The 95% confidence interval on the proportion of such graduates planning to continue their education is (0.2036, 0.2798).
(C) Compare your answers to parts (a) and (b) and explain why they are the same or different.
The margin of error of a confidence interval of proportions is:
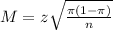
This means that, due to higher value of z, a 95% confidence interval, as in part b, is wider than a 90% confidence interval, found in part a, and is the difference between these two intervals.
(D) Could you use either of these confidence intervals to determine whether the proportion is actually 0.25? Explain your answer. Hint: Use the normal approximation to the binomial.
Yes, because 0.25 is inside both intervals.