To get the slope of this function, let's rewrite in the slope-intercept form.
The slope-intercept form have the following form:
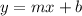
where 'm' represents the slope and 'b' represents the y-intercept.
We have the following function
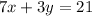
To rewrite in the slope-intercept form, we start with our original equation
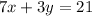
Then, we can subtract '7x' from both sides:
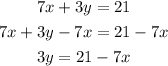
And then, finally, divide both sides by 3.
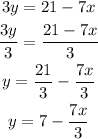
And with this, we have our final equation
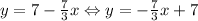
Done! If you compare this last equation with the general form of the line, you're going to find:
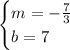
Where 'm' is the slope, and 'b' the y-intercept.