Question

-Exponential and Logarithmic Functions- Find the current yearly rate of increase and estimate the population 10 yr from now if the trend continues.

Answer 1

the current yearly rate of increase is 2.5%

The population 10 years from now is 1920 (to the nearest whole number)

Step-by-step explanation:

The population two years ago = 1500 (initial value)

The present population (2 years after) = 1576

We can find the rate of increase using the information above:

Two points (0, 1500) and (2, 1576)

`\begin{gathered} \text{slope = }(1576-1500)/(2-0) \\ \text{slope = 76/2} \\ \text{slope = 38} \end{gathered}`
`\begin{gathered} \text{The yearly rate of increase = }\frac{rate}{in\text{itial population}} \\ \text{The yearly rate of increase = }(38)/(1500) \\ \text{The yearly rate of increase = }0.025\text{ = 2.5\%} \end{gathered}`
`\begin{gathered} U\sin g\text{ exponential function:} \\ y=a(1+r)^t\text{ (since the population is increasing)} \\ a\text{ = initial value} \\ r\text{= rate of increase per year = 2.5\%} \\ t\text{ = time} \end{gathered}`
`\begin{gathered} a\text{ = 1500} \\ r\text{ = 2.5\% = 0.025} \\ t\text{ = 10 years} \\ y\text{ = 1500(1+}0.025)^(10) \\ y=1500(1.025)^(10) \\ y\text{ = }1920.13 \end{gathered}`

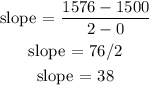
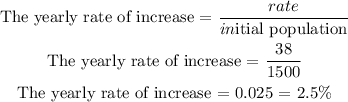
Hence, the current yearly rate of increase is 2.5%

The population 10 years from now is 1920 (to the nearest whole number)