The vertices of the given figure are:
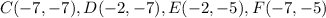
Recall that the coordinate rule for 270⁰ clockwise rotation around the origin is:
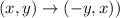
Apply this rule to the first vertex C(-7,-7):
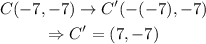
Apply the same rule to other vertices to get:
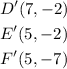
Answer:
C'=(7,-7)
D'=(7,-2)
E'=(5,-2)
F'=(5,-7)