Question

Can you help me with this answer

Answer 1

B is correct, and D is correct

if you multiply 3 times 5 you get 15 m which is the area for the rectangle, then you have to find the area for the triangle, which you would have to multiply 6 times 5 which you get 30, then divide 30 by 2, which would be 15!

Explanation:

Answer 2

B and D are correct.

Explanation:

To find the area of a rectangle, simply multiply its length by its width. In this case, the length of the rectangle is
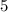`5` m and the width of the rectangle is
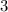`3` m, so its area must be
`5*3=15` square meters.

To find the area of a triangle, divide the product of the triangle's base and height by
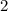`2`. As an algebraic expression, that would be
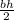`(bh)/(2)`, where
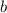`b` and
`h` are the triangle's base and height, respectively. In this case,
`b=6` and
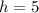`h=5`, so the triangle's area is
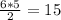`(6*5)/(2)=15` square meters.

Now, let's look at the statements.

A: The triangle's area is
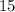`15` square meters, not
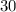`30`, so A is incorrect.

B: The rectangle's area is
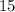`15` square meters and the triangle's area is also
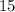`15` square meters. Because the two figures have the same areas, their areas are equal, so B is correct.

C: We've already established that the two figures have equal areas, so one can't have a greater area than the other. Therefore, C is incorrect.

D: The rectangle's area is indeed
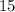`15` square meters, so D is correct.

Hope this helps!