Question

Please help me with this problem:A model rocket is launched from the ground with an initial velocity of 80 feet per second. The height of an object h, in feet, after t seconds, with initial velocity v0 and initial height h0 is given by h(t) = −16t^2 + v0t + h0.What is the approximate maximum height the rocket reaches?Enter your answer in the box. ___ ft

Answer 1

Given the function

`h(t)=-16t^2+v_0t+h_0`

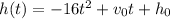
Notice that its graph is a parabola that opens downwards; therefore, its maximum is equal to its only critical point.

Furthermore, according to the question, the initial velocity of the rocket is 80ft/sec and its initial height is 0ft (ground level); then,

`\begin{gathered} v_0=80,h_0=0 \\ \Rightarrow h(t)=-16t^2+80t \end{gathered}`

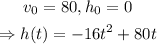
To find its critical point, solve the equation h'(t)=0 for t, as shown below

`\begin{gathered} h^(\prime)(t)=2*-16t+80=-32t+80 \\ \Rightarrow h^(\prime)(t)=0 \\ -32t+80=0 \\ \Rightarrow t=(80)/(32)=2.5 \end{gathered}`

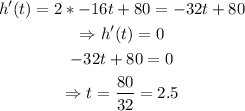
Finding h(2.5)

`\Rightarrow h(2.5)=-16(2.5)^2+80*2.5=-100+200=100`

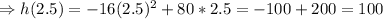
Therefore, the maximum height is 100ft (at t=2.5 seconds)