Using the given histogram which shows the amount invested each year, let's solve for the following:
• (a). Draw a table to show the amounts invested each year.
Using the graph, we have the table:
Year Amount invested ($)
1985 3300
1986 3800
1987 4300
1988 4800
1989 5300
• (b). Let's construct a line graph representing the data.
To construct a line graph, let's create points using the values in the table.
Let x be the number of years after 1985.
We have the points:
(x, y) ==> (0, 3300), (1, 3800), (2, 4300), (3, 4800), (4, 5300)
Plot the points and connect them using a straight line.
• (c). Since the graph is a linear graph, it means it has a constant rate of change.
Therefore, the increase each year is constant.
• (d). The value of increase in investment.
Here, we are to use the slope formula.
Apply the slope formula:

Take any two points representing the data:
(x1, y1) ==> (0, 3300)
(x2, y2) ==> (2, 4300)
Plug in the values in the equation and solve for slope, m:
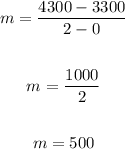
The slope is 500.
This means the investment increased constantly by $500 each year.
• ANSWER:
(a). Table:
Year Amount invested ($)
1985 3300
1986 3800
1987 4300
1988 4800
1989 5300
(b). The graph is above.
(c). The increase each year is constant.
(d). The investment increased by $500 each year.