Given
The engines of a plane are pushing it due north at a rate of 300 mph, and the wind is pushing the plane 20° west of north at a rate of 40 mph.
To find the magnitude of the resultant vector.
Step-by-step explanation:
It is given that,
Then,
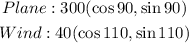
That implies,
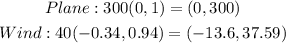
Adding these two points implies,
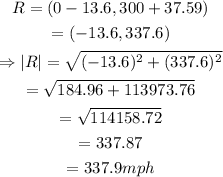
Hence, the magnitude of R is 337.9mph.