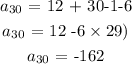Question

What is the value of the 30th term in the following arithmetic sequence?12, 6, 0, -6, ...-186342186-162

Answer 1

`-162`

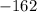
Step-by-step explanation:

Here, we want to get the value of the 30th term of the sequence

Mathematically, the nth term of an arithmetic sequence can be calculated using the formula:

`a_n=\text{ a+ \lparen n-1\rparen d}`

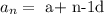
where a is the first term which is 12

d is the common difference which is the difference between terms (6-12 = 0-6 = -6-0 = -6)

n is the number of terms which is 30

Substituting the values, we have it that:

`\begin{gathered} a_(30)\text{ = 12 + \lparen30-1\rparen-6} \\ a_(30)\text{ = 12 -\lparen6}*29) \\ a_(30)\text{ = -162} \end{gathered}`