Probability Density Function
It's a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would be close to that sample.
The total probability of the density function must be 1.
We are given the probability density function by:

The total probability of this function can be calculated as the definite integral:
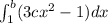
Integrating:
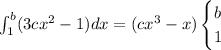
(sorry for the lack of an adequate vertical bar)
Thus the integral is:
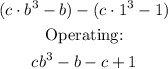
Equating to 1:

Factoring:
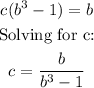
Note the value of b must be greater than 1