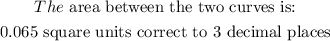Question

Hi there, I need assistance in solving this calc-12 question relating to the area between curves

Answer 1

Step 1:

In this question, we are given the following:

Step 2:

The details of the solution are as follows:

`\begin{gathered} Given\text{ that:} \\ y\text{ = }√(5x)\text{ --equation 1} \\ and\text{ } \\ y\text{ = 4x - equation 2} \\ Then,\text{ the intersection will be:} \\ \end{gathered}`
`\begin{gathered} √(5x)\text{ = 4x } \\ square\text{ both sides, we have that:} \\ 5x=16x^2 \\ Then,\text{ this means that:} \\ 5\text{ x - 16 x}^2\text{ = 0} \\ and \\ x\text{ \lparen 5 - 16x \rparen = 0} \\ x\text{ = 0 or 5 - 16 x = 0} \\ x\text{ = 0 or 16x = 5} \\ x\text{ = 0 or x =}(5)/(16) \end{gathered}`
`\begin{gathered} Then\text{ , } \\ a\text{ = 0} \\ b\text{ = }(5)/(16) \end{gathered}`

PART TWO:

Between these two points, the curve that takes on smaller values is:

`y_1=√(5x)`

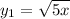
and the curve that takes on the larger values is:

`y_2=\text{ 4x}`

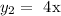
Thus, to find the area of the region, we must calculate the integral:

`\int_a^by_2-y_1\text{ dx}`

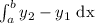
So, the area between the two curves is:

`\begin{gathered} The\text{ area between the two curves is:} \\ 0.065\text{ square units \lparen correct to 3 decimal places\rparen} \end{gathered}`