step 1
In the right triangle ABD
Applying the Pythagorean Theorem
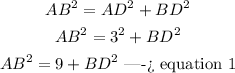
step 2
In the right triangle BCD
Applying the Pythagorean Theorem
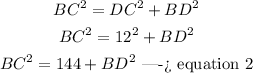
step 3
In the right triangle ABC
Applying the Pythagorean Theorem
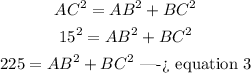
substitute equation 1 and equation 2 in equation 3
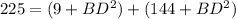
Solve for BD
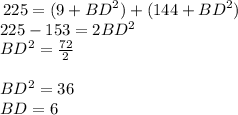
The answer is the option C