Question

Please help me with this problem so I can help my son. I have attached the image of the problem from his homework paper that he was working on in class please help.

Answer 1

`(2x-3)(x+2)`

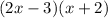
1) Let's factor this quadratic, by rewriting that coefficient "b" as -4x+2x, this is possible since we have the coefficient a greater than 1 and by doing that we can write coefficients that share divisors with the leading coefficient 2 and the coefficient c = 12

`\begin{gathered} 2x^(2)-2x-12=0 \\ 2(x^2-x-6)=0 \\ 2(x^2+2x-3x-6)=0 \\ 2x(x^{}+2)-3(x+2) \\ (2x-3)(x+2) \end{gathered}`

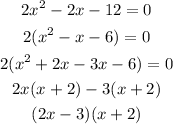
Note that when we find a repetition (x+2) on both factors then we can rewrite as a product.