The domain of a function is all the x values that x can take.
We have the next function:
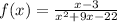
Now, we need to find when the denominator is undefined.
The denominator can be 0.
So equal the whole expression to 0.
Therefore:
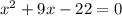
To find the x value, use the quadratic formula, which is given by:
![x=\frac{-b\pm\sqrt[2]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/vecqv42h8re9tvnbp43529x5x01l9ve2cf.png)
Replace this values using a=1, b=9 and c= -22
![x=\frac{-9\pm\sqrt[]{9^2-4(1)(-22)}}{2(1)}](https://img.qammunity.org/2023/formulas/mathematics/college/f6yu1o0f7651socgidip2qn8abcg7ka7vd.png)
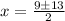
Then x will take two values:
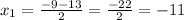
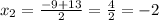
So, when x= -11 and x=2, the function is undefined.
Finally, we can find the domain: (-inf, -11) U (-11,2) U (2, inf)