Question

Please review pictures attached.Thank you Which graph best represents the solution to this system of inequalities?

Answer 1

Given inequalities:

`\begin{gathered} \text{x + y }\leq\text{ 6} \\ x\text{ + 2y }\leq\text{ 8} \end{gathered}`

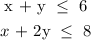
We would be plotting the graph of each inequality combine their solutions.

`x\text{ + y }\leq\text{ 6}`

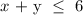
We have the equation : x + y = 6 from the inequality

We need two points to draw thw boundary line. Hence:

When x = 0:

`\begin{gathered} 0\text{ + y = 6} \\ y\text{ =6} \end{gathered}`

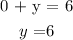
When y = 0:

`\begin{gathered} x\text{ + 0 = 6} \\ x\text{ =6} \end{gathered}`

We have the points : (0,6) and (6,0)

Now that we have the boundary line points, we can show the region that satisfies the inequality as shown below:

The shaded region is the solution to the inequality

Similarly for the second inequality:

`x\text{ + 2y }\leq\text{ 8}`

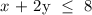
We need two points to draw the boundary line: x + 2y = 8. Hence:

When x = 0:

`\begin{gathered} 0\text{ + 2y = 8} \\ \text{Divide both sides by 2} \\ y\text{ =4} \end{gathered}`

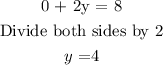
When y = 0:

`\begin{gathered} x\text{ + 2}*0\text{ = 8} \\ x\text{ +0 = 8} \\ x\text{ =8} \end{gathered}`

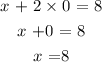
We have the points: (0,4) and (8,0)

Now that we have the boundary line points, we can show the region that satisfies the inequality as shown below:

The shaded region is the solution to the inequality

Combining the solutions, we have:

Hence, the graph that best represents the solution to the system of inequalities is the graph in Option D

Answer: Option D