Question

The extract of a plant native to Taiwan has been tested as a possible treatment for Leukemia. One of the chemical compounds produced from the plant was analyzed for a particular collagen. The collagen amount was found to be normally distributed with a mean of 65 and standard deviation of 7.7 grams per mililiter. Round all answers to 4 decimal places.

Required:
a. What is the probability that the amount of collagen is greater than 60 grams per.
b. What is the probability that the amount of collagen is less than 90 grams per.
c. What percentage of compounds formed from the extract of this plant fall within 1 standard deviation of the mean?

Answer 1

a) 0.2578 = 25.78% probability that the amount of collagen is greater than 60 grams per mililiter.

b) 0.9994 = 99.94% the probability that the amount of collagen is less than 90 grams per mililiter.

c) 68.26% of compounds formed from the extract of this plant fall within 1 standard deviation of the mean

Explanation:

Normal Probability Distribution:

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
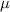`\mu` and standard deviation
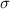`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

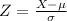
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

The collagen amount was found to be normally distributed with a mean of 65 and standard deviation of 7.7 grams per mililiter.

This means that
`\mu = 65, \sigma = 7.7`

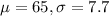
a. What is the probability that the amount of collagen is greater than 60 grams per.

This is 1 subtracted by the pvalue of Z when X = 60. So

`Z = (X - \mu)/(\sigma)`

`Z = (60 - 65)/(7.7)`

`Z = -0.65`

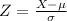
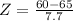
`Z = -0.65` has a pvalue of 0.2578

0.2578 = 25.78% probability that the amount of collagen is greater than 60 grams per mililiter.

b. What is the probability that the amount of collagen is less than 90 grams per.

This is the pvalue of Z when X = 90.

`Z = (X - \mu)/(\sigma)`

`Z = (90 - 65)/(7.7)`

`Z = 3.25`

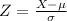
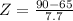
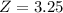
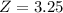`Z = 3.25` has a pvalue of 0.9994

0.9994 = 99.94% the probability that the amount of collagen is less than 90 grams per mililiter.

c. What percentage of compounds formed from the extract of this plant fall within 1 standard deviation of the mean?

Between Z = 1 and Z = -1, so the proportion is the pvalue of Z = 1 subtracted by the pvalue of Z = -1

Z = 1 has a pvalue of 0.8413

Z = -1 has a pvalue of 0.1587

0.8413 - 0.1587 = 0.6826

0.6826*100% = 68.26% of compounds formed from the extract of this plant fall within 1 standard deviation of the mean