Answer:
The estimated evaporation is 51340 cubic meters.
Step-by-step explanation:
Let suppose that precipitation is very small in comparison with depth of the Clear Lake. The monthly change in the volume of the lake (
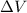 ), in cubic meters, is estimated by the following formula:
), in cubic meters, is estimated by the following formula:
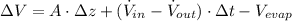 (1)
(1)
Where:
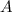 - Surface area of the lake, in square meters.
- Surface area of the lake, in square meters.
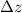 - Water precipitation, in meters.
- Water precipitation, in meters.
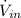 - Average water inflow, in cubic meters per second.
- Average water inflow, in cubic meters per second.
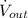 - Average water outflow, in cubic meters per second.
- Average water outflow, in cubic meters per second.
 - Monthly time, in seconds.
- Monthly time, in seconds.
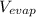 - Evaporation, in cubic meters.
- Evaporation, in cubic meters.
If we know that
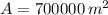 ,
,
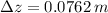 ,
,
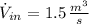 ,
,
 ,
,
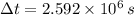 and
and
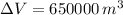 , then the estimated evaporation is:
, then the estimated evaporation is:
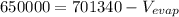 (2)
(2)
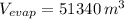
The estimated evaporation is 51340 cubic meters.