Given:
Diameter of the softball = 3.8 inches
Let's estimate the amount of leather used to cover the softball.
A softball has the shape of a sphere.
To find the amount of leather used to cover the softball, let's find the surface area of the softball.
To find the surface area, apply the formula for the surface area of a sphere:
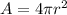
Where:
r is the radius.
To find the radius, we have:
radius = diameter/2 = 3.8/2 = 1.9 inches
Now, to find the surface area, we have:

Therefore, the amount of leather used to cover the softball is 45.4 square inches.
ANSWER:
45.4 in²