Step 1
Write the system of equations required to solve the problem

Step 2
Find the value of x using the substitution method
Find the value of y from equation 2
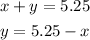
Substitute for y as seen above in equation 1
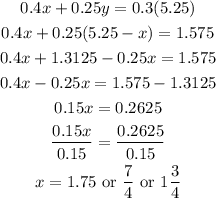
Step 3
Find the value of y by substituting for x in equation 2
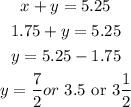
Therefore,
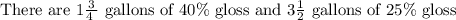
The answer is, therefore, option C