Given:
Two intercept points be (-2,0) and (4,0) and passing through the point (1,-27).
Let the equation of parabola be
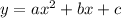
Substituting the points we get,
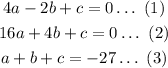
Solving (1) and (2) we get,
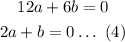
Solving (2) and (3) we get,
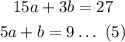
Solving (4) and (5)
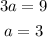
Substituting a=3 in (4)
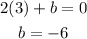
Substitute a=3 & b=-6 in (1)
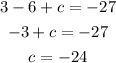
Equation of parabola is
