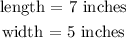Answer:
The dimensions of the rectangle are 7 inches by 5 inches;
Step-by-step explanation:
Given that the length of a rectangle is 8 inches shorter than three times its width.
Let x represent its length and w represent its width.

If the area of the rectangle is 35 square inches;
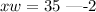
Making w the subject of formula in equation 2;
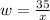
substituting into equation 1;
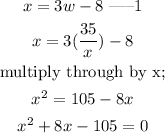
Solving for x in the quadratic equation;
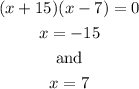
Since length cannot be negative;
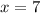
substituting to equation 2;
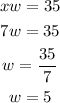
Therefore, the dimensions of the rectangle are 7 inches by 5 inches;