Question

For the following, graph the system of inequalities. Name the coordinates of the vertices of the feasible region. Find the maximum and minimum values of the given function for this region.

Answer 1

Region 1)

`y\ge-x-2`

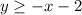
Y(x=0) = -2

X(y=0) = -2

For region 1 we need to draw a line that crosses (-2,0) and (0,-2), and select the right hand side. Like this...

Region 2)

`y\ge3x+2`

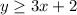
For region 2 we need to draw a line from (0,2) to (-2,-4) and select the region to the left hand side or upwards.

Y(x=0) = 2

X(y=-2) = -4

Let me add an image...

Region 3)

`y\leq x+4`

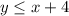
For region 3 we need to draw a line that crosses (-4,0) and (0,4) and we select the region to the right hand side, as I'll show you

Now we can see the feasible region. Let's find the coordinates of the vertices...

Our first vertex is where line blue and green intercept... this is, where

y = 3x + 2 and y = x + 4

3x + 2 = x + 4

3x - x = 4 - 2

2x = 2

x = 1 ; Then y = 3*(1) + 2 = 3 + 2 = 5

Vertex 1 ) (x,y) = (1,5)

Vertex #2 is where the red and the green lines intercept:

y = -x -2 ; y = x + 4

x + 4 = -x - 2

x + x = -2 - 4

2x = -6

x = -6/2 = -3 ; Then y = (-3) + 4 = -3 + 4 = 1

Vertex 2) (x,y) = (-3,1)

Vertex #3 is where the red and blue lines intercept:

y = -x - 2 ; y = 3x + 2

-x - 2 = 3x + 2

-x - 3x = 2 + 2

-4 x = 4

x = -4 / 4 = -1 ; So, y = 3*(-1) + 2 = -3 + 2 = -1

Vetex 3) (x,y) = (-1,-1)

Now, we let's add the given equation to the graph...

f(x,y) = -3x + 5y = 0

5y = 3x + 0

y = 3/5 * X + 0

Interpt when Y=0 is 0

the slope m = 3/5

we can to draw a line from (0,0) to (-10,-6)

Now, let's see how it would look like into the feasible region...

We can see that the maximun value is where the function intercepts the blue line or the line of the second region

y = 3/5 * x ; y = 3x + 2

3/5 x = 3x + 2

(3/5 - 3) x = 2

-12/5 * x = 2

x = -5/6 ; thus y = 3/5 * (-5/6) = -1/2

Therefore the maximun is located in (x,y) = (-5/6 , -1/2)

Now, the minimun is located where the function intercepts the red line

y = 3/5 * x ; y = -x -2

3/5 x = -x - 2

(3/5 + 1) * x = -2

8/5 x = - 2

x = -2*(5/8) = -5/4 ; y = 3/5 * (-5/4) = -3/4

Therefore the minimun is located in (x,y) = (-5/4 , -3/4)