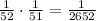In a deck of cards, there are 4 aces, 4 ones, 4 twos,... 4 Jacks, 4 queens, and 4 kings; 52 cards in total.
a) There are 4 aces in total in the deck and 52 total cards; therefore,
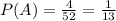
b)
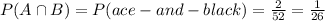
c)
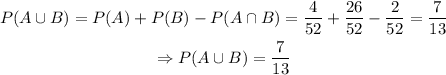
d)
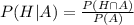
and
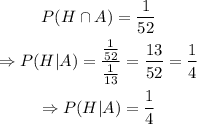
e)
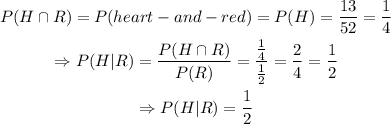
f)
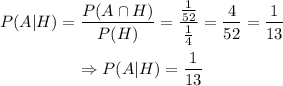
The only event with those characteristics (picking a red ace first and then a heart ace) is when we draw a diamond ace first and then a heart ace. The probability of this event is