Remember that
You can verify if a set of vectors is linearly independent by computing the determinant of a matrix whose columns are the vectors you want to check.
They are linearly independent if, and only if, this determinant is not equal to zero.
so
we have
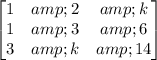
The determinant of the given matrix is calculated as
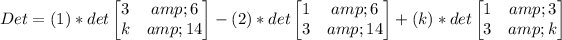
![Det=(1)*[14*3-6*k]-(2)*[14*1-6*3]+(k)*[k*1-3*3]](https://img.qammunity.org/2023/formulas/mathematics/college/24u55expg4wvt108cpwslmmakupp1b540q.png)
![\begin{gathered} Det=(1)*[42-6k]-(2)*[14-18]+(k)*[k-9] \\ Det=42-6k+8+k^2-9k \\ Det=k^2-15k+50 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/o4fb96v0dptjxw6bhja06wra0kaujgtj62.png)
Equate to zero the quadratic equation
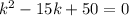
Solving by the formula
a=1
b=-15
c=50
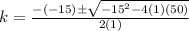
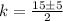
The values of k are
k=10 and k=5
Therefore
The values of k are 5 and 10