Question

A given bacteria culture initially contains 2000 bacteria and doubles every half hour. The number of bacteria p at a given time t is given by the formula p(t)=2000e^kt for some constant k. (You will need to find k to answer the following)A) find the size of the bacterial population after 20 minutes. B) find the size of the bacterial population after 6 hours.

Answer 1

Now, we know that the culture initially contains 2000 bacteria and that it doubles every half hour. Assuming that the time t is in hours, this would mean that

`p(0.5)=4000=2000e^(0.5k)`

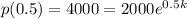
Solving for k,

`\begin{gathered} 4000=2000e^(0.5k) \\ \rightarrow2=e^(0.5k) \\ \rightarrow\log (2)=\log (e^(0.5k)) \\ \rightarrow\log (2)=0.5k\log (e) \\ \rightarrow k=(\log (2))/(0.5) \\ \\ \Rightarrow k=2\log (2) \end{gathered}`

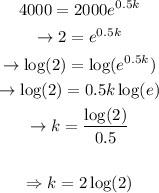
This way, we would have that:

`p(t)=2000e^(2\log (2)\cdot t)`

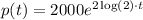
A)

20 minutes is 1/3 of an hour. This way,

`\begin{gathered} p((1)/(3))=2000e^{2\log (2)\cdot(1)/(3)} \\ \\ \Rightarrow p((1)/(3))=3174.80 \end{gathered}`

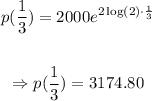
Thereby, the bacterial population after 20 minutes is 3,174.80

B)

`\begin{gathered} p(6)=2000e^(2\log (2)\cdot6) \\ \Rightarrow p(6)=8192000 \end{gathered}`

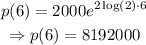
Thereby, the bacterial population after 6 hours is 8,192,000