Given:
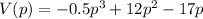
Take the derivative with respect to p,
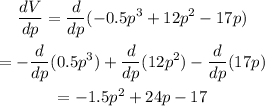
Now set the derivative equal to zero,
![\begin{gathered} (dV)/(dp)=0 \\ -1.5p^2+24p-17=0 \\ p=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a},a=-1.5,b=24,c=-17 \\ p=\frac{-24\pm\sqrt[]{24^2-4(-1.5)(-17)}}{2(-1.5)} \\ p=\frac{-24\pm\sqrt[]{474}}{-3} \\ p=\frac{-24+\sqrt[]{474}}{-3},p=\frac{-24-\sqrt[]{474}}{-3} \\ p=\frac{24-\sqrt[]{474}}{3},p=\frac{24+\sqrt[]{474}}{3} \\ p=0.7428,p=15.2572 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/n2zrlcgfxg8dsq6gu1yhi9ua5e29ztpr14.png)
Now, take second derivative of the function,
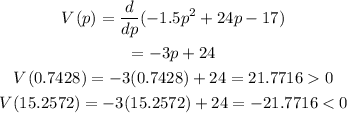
As the second derivative is less than 0 when p=15.2572 that is maximum profit.
So, the price charge to maximize its profit is p=15.2572 ( approximated)