Answer
False.
If the polynomial has an even degree, then it is not necessarily an even function.
Explanation
Let's take for example the next even degree polynomial:
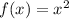
In even functions, the next condition must be satisfied:
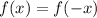
Evaluating f(-x) in this case:
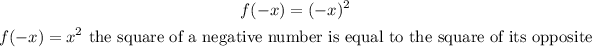
Then, f(x) = x² is even.
Now, let's analyze the next even degree polynomial:
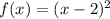
Evaluating this function at x = -1 and x = 1, we get:

In conclusion, f(x) = (x - 2)² is not even.