The Vertical Line Test of a Function
When the graph of a function is given, we can use the vertical line test to find if it's a function or not.
Recall a function must satisfy the condition that for any value of x there should be only one value of y.
If we draw a vertical line and the graph of the function is intercepted (or touched) by the line more than once, then it's not the graph of a function.
We are given the equation:
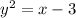
Solving for x:
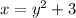
Let's give y the values: y={-2, -1, 0, 1, 2} and calculate x.
For y=2 and y=-2 we get the same value for x because any number squared is positive:
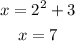
Thus we have the points (7,2) and (7,-2)
For y=1 and y=-1 we get the points (4,1) and (4,-1)
For y=0 we have the point (3,0).
The graph is shown below:
As seen, it's possible to draw a vertical line that intercepts the graph twice. Thus the graph does not correspond to a function