Answer:
1. The elastic potential energy is 0.0176 Joules
2. The kinetic energy of the pinball the instant it leaves the spring is 0.0176 Joules
3. The speed of the pinball the instant it leaves the spring is approximately 2.42212 m/s
4. The height of the part where the pinball is located on the machine above the ground is approximately 0.213 meters
Step-by-step explanation:
The spring constant of the pinball machine's plunger, k = 22 N/m
The amount by which the pinball machine's plunger is compressed, x = 0.04 m
The mass of the pinball ball, m = 0.006 kg
1. The elastic potential energy, P.E. = 1/2·k·x²
By substitution, we get;
P.E. = 1/2 × 22 N/m × (0.04 m)² = 0.0176 J
The elastic potential energy, P.E. = 0.0176 J
2. At the instant the pinball leaves the spring, the plunger and therefore the force of the plunger no longer acts on the pinball
Since there are no external forces acting on the pinball to increase the speed of the pinball after it leaves the spring, the velocity reached is its maximum velocity, and therefore, the kinetic energy, K.E. is the maximum kinetic energy which by the conservation of energy, is equal to the initial potential energy
Therefore;
K.E. = P.E. = 0.0176 J
The kinetic energy of the pinball the instant it leaves the spring, K.E.= 0.0176 J
3. The kinetic energy, K.E., is given by the following formula;
K.E. = 1/2·m·v²
Where;
v = The speed or velocity of the object having kinetic energy K.E.
Therefore, from K.E. = 0.0176 J, and by plugging in the values of the variables, we have;
K.E. = 0.0176 J = 1/2 × 0.006 kg × v²
v² = 0.0176 J/(1/2 × 0.006 kg) = 88/15 m²/s²
v = √(88/15 m²/s²) ≈ (2·√330)/15 m/s ≈ 2.42212 m/s
The speed of the pinball the instant it leaves the spring, v ≈ 2.42212 m/s
4. The height of the pinball is given by the following kinematic equation of motion;
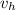 ² = u² - 2·g·h
² = u² - 2·g·h
Where;
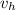 = The velocity of the pinball at the given height = 1.3 m/s
= The velocity of the pinball at the given height = 1.3 m/s
u = v ≈ 2.42212 m/s (The initial velocity of the pinball as it the spring)
g = The acceleration due to gravity ≈ 9.8 m/s²
h = The height of the pinball above the ground
We get;
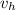 ² = 1.3² = 2.42212² - 2 × 9.8 × h
² = 1.3² = 2.42212² - 2 × 9.8 × h
∴ h = (2.42212² - 1.3²)/(2 × 9.8) ≈ 0.213
The height of the part where the pinball is located on the machine above the ground, h ≈ 0.213 m