Question

Write the equation of the line that passes through (2,5) and (2,-13).

Answer 1

To find the equation of the line that passes through these points you can first find the slope of the line using this formula:

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where }(x_1,y_1)\text{ and }(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`

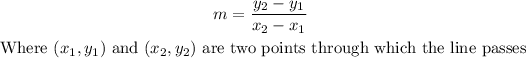
In this case, you have

`\begin{gathered} (x_1,y_1)=(2,5) \\ (x_2,y_2)=(2,-13) \end{gathered}`
`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(-13-5)/(2-2) \\ m=(-18)/(0) \end{gathered}`

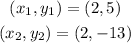
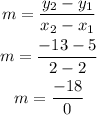
Since it is not possible to divide by zero then the slope of this line is not defined. Then the line through the given points is a vertical line.

By definition, the slope of a vertical line is not defined, and its representation is indicated by the coordinate where it crosses the x-axis.

Therefore, the equation of the line that passes through the given points is:

`x=2\text{ }`

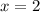
As you can see in the following graph