Given;
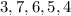
STEP 1:
We need to find the mean of the data above
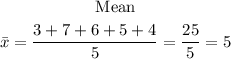
STEP 2: We need to get the sum of the square of the difference of each data from the mean.
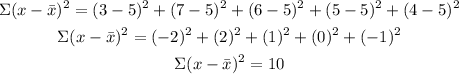
STEP 3: We can find the standard deviation of the data using the formula below;
![\begin{gathered} \text{standard deviation }\sigma=\sqrt[]{\frac{\Sigma(x-\bar{x})^2}{n}} \\ \text{Where n is the number of data = 5} \\ \sigma=\sqrt[]{(10)/(5)} \\ \sigma=\sqrt[]{2} \\ \sigma=1.41 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/by7nsmyto2k746a1mh3jf6w4qh9grzlr9k.png)
Hence, the standard deviation for the group of data to the nearest hundredth is 1.41