This is a question asking you to pick 3 fruits from an array of 7 different fruits.
This means we can use combination to solve this question.
To pick r things from a set of n things:
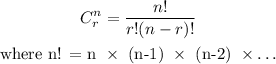
Thus, to pick 3 fruits from a set of 7 fruits:
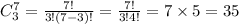
Therefore, the number of ways to pick 3 fruits from 7 fruits is = 35 ways