The equation that defines the motion is given as:
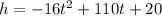
To find when the height will be 59 feet, substitute h=59 into the equation and solve for t:
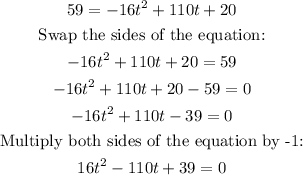
Solve the quadratic equation using any method of your choice.
Using the quadratic formula where a=16, b=-110 and c=39:
![\begin{gathered} t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ t=\frac{-(-110)\pm\sqrt[]{(-110)^2-4(16)(39)}}{2(16)} \\ t=\frac{110\pm\sqrt[]{12100-2496}}{32} \\ t=\frac{110\pm\sqrt[]{9604}}{32}_{} \\ t=(110\pm98)/(32) \\ t=(208)/(32)or\text{ }(12)/(32) \\ t=6.5s\text{ or }0.375s \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ymi841iea9b48jm4lleewtjgyhqn57reqd.png)
The unit of time is seconds.
T
The object will reach the ground when the height is zero, that is when h=0.
Substitute into the equation and solve for t again:
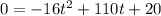
Using the same procedure, where a=-16, b=110 and c=20, use the quadratic formula to solve for t to get:

Since time cannot be negative, discard the negative value. So, the object will reach the ground at about t=7.05 seconds.