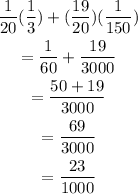Question

13. In a certain population of caribou, the probability of an animal's being sickly is 1/20. If a caribou is sickly, the probability of its being eaten by wolves is 1/3. If a caribou is not sickly, the probability of its being eaten by wolves is 1/150. If a caribou is chosen at random from the herd, what is the probability of the event that it will be eaten by wolves?

Answer 1

This is a multi step problem. Let's take the First Step:

P(sickly) = 1/20

P(not sick) = 1 - 1/20 = 19/20

Thus,

P(sick) = 1/20

P(not sick) = 19/20

Given sick,

P(eaten) = 1/3,

P(not eaten) = 1 - 1/3 = 2/3

Thus, Given Sick,

P(eaten) = 1/3

P(not eaten) = 2/3

Then, given not sick,

P(eaten) = 1 /150

P(not eaten) = 1 - (1/150) = 149/150

Thus, given not sick,

P(eaten) = 1/150

P(not eaten) = 149/150

Now, we want probabilty that it will be eaten. What are the ways?

(sick and eaten) or (not sick and eaten)

In probability, "and" means multiplication and "or" means addition!!

Thus, we can say:

P(sick) x P(sick, eaten) + P(not sick) x P(not sick, eaten)

So, let's calculate:

`\begin{gathered} (1)/(20)((1)/(3))+((19)/(20))((1)/(150)) \\ =(1)/(60)+(19)/(3000) \\ =(50+19)/(3000) \\ =(69)/(3000) \\ =(23)/(1000) \end{gathered}`