Question

Ed Moura has $72000 invested in stocks paying 9%. How much additional money should he invest in certificates of deposit paying 6% so that the average return on the two investments is 7%?

Answer 1

Hello there. To solve this question, we'll have to remember some properties about investments.

Consider this is a simple investment, such that for a principal value P invested at an interest rate r for a period of t (say, years, months, so on...), the interest earned is given by

`I=P\cdot r\cdot t`

This can be interpreted as the return of this investment due to the interest rate r.

Now, we want to determine a value x for which when investing this value at an interest rate of 6%, considering Ed Moura's other $72000 investment paying 9%, he has an average return of 7%.

For this, we assume that for a certain period of time t

`\begin{gathered} I_1:\text{ investment in stocks given by }72000\cdot0.09\cdot t \\ I_2:\text{ investment in certificates given by }x\cdot0.06\cdot t \\ \text{total investment }=72000+x \\ \text{ Average return }=(72000+x)\cdot0.07\cdot t \\ \end{gathered}`

Such that we get

`\begin{gathered} Avg=(I_1+I_2)/(2) \\ \\ \Rightarrow(72000+x)\cdot0.07\cdot t=(72000\cdot0.09\cdot\,t+x\cdot0.06\cdot\,t)/(2) \\ \\ (72000+x)\cdot0.07\cdot t=36000\cdot0.09\cdot\,t+x\cdot0.03\cdot\,t \end{gathered}`

Simplify the equation by a factor of t, t > 0

`(72,000+x)*0.07=36,000*0.09+x*0.03`

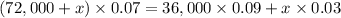
Expand the left hand side