Question

I need help with this, having trouble solving It is a practice trigonometry problem from my ACT prep guide

Answer 1

Given the expression:

`(\tan(-(2\pi)/(3)))/(\sin((7\pi)/(4)))-\sec (-\pi)`

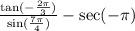
Let's find the exact value of the expression.

• First rewrite tan(-2π/3) in terms of sines and cosines.

We have:

`((\sin(-(2\pi)/(3)))/(\cos(-(2\pi)/(3))))/(\sin((7\pi)/(4)))-\sec (-\pi)`

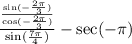
• Now, rewrite in product form:

`\begin{gathered} (\sin(-(2\pi)/(3)))/(\cos(-(2\pi)/(3))*\sin((7\pi)/(4)))-\sec (-\pi) \\ \\ \end{gathered}`

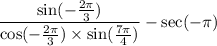
Apply the reference angles by finding the angle suing the equivalent trigonomteric values.

We have:

`\begin{gathered} (\sin((4\pi)/(3)))/(\cos((4\pi)/(3))(-\sin((\pi)/(4)))-\sec (-\pi) \\ \\ (-\sin((\pi)/(3)))/(-\cos((\pi)/(3))(-(\sin\pi)/(4)))-\sec (-\pi) \end{gathered}`

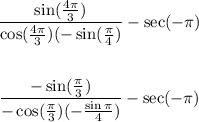
Substitute each trig value with the exact value:

`\begin{gathered} \frac{-\frac{\sqrt[]{3}}{2}}{-(1)/(2)*(-1\frac{\sqrt[]{2}}{2})}-\sec (-\pi) \\ \\ \frac{-\frac{\sqrt[]{3}}{2}}{-((-1)/(2)*\frac{\sqrt[]{2}}{2})_{}}-\sec (-\pi) \\ \\ \frac{-\frac{\sqrt[]{3}}{2}}{-(-\frac{\sqrt[]{2}}{4})}--\sec (0) \\ \\ \frac{-\sqrt[]{3}*4}{2*\sqrt[]{2}}--\sec (0) \\ \\ \frac{-2\sqrt[]{3}}{\sqrt[]{2}}--\sec (0) \\ \\ \end{gathered}`

Rationalize the denominator:

`\begin{gathered} \frac{-2\sqrt[]{3}}{\sqrt[]{2}}*\frac{\sqrt[]{2}}{\sqrt[]{2}}+\sec (0) \\ \\ -\sqrt[]{3*2}+\sec (0) \\ \\ -\sqrt[]{6}+\sec (0) \end{gathered}`

Where:

sec(0) = 1

`\begin{gathered} -\sqrt[]{6}+1 \\ \\ \end{gathered}`

ANSWER:

`\begin{gathered} \\ -\text{ }\sqrt[]{6}+1 \end{gathered}`