Question

Identify A and B, factor completely and find the real roots

Answer 1

The given equation is:

`x^3+64=0`

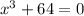
The equation is a sum of two(2) cubes which can be further simplified to be:

`x^3+4^3=0`

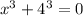
i) Hence, a=x and b=4

Factorization of sum of two(2) cubes is given by the equation;

`x^3+y^3=(x+y)(x^2-xy+y^2)`

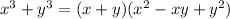
Relating this to the given equation, we have:

`\begin{gathered} x^3+64=0 \\ x^3+4^3=0 \\ \Rightarrow(x+4)(x^2-4x+16)=0 \end{gathered}`

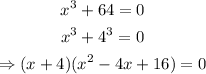
ii) Hence, the factor completely is:

`(x+4)(x^2-4x+16)=0`

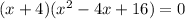
iii) To find the real root,we have;

`\begin{gathered} x+4=0 \\ x=-4 \end{gathered}`

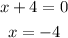
Hence, the real root is x = -4