Question

IFactorial expressionsEvaluate.(4!6!)/(2!5!)Simplify your answer as much as possible.I need help with this math problem.

Answer 1

Step-by-step explanation

The factorial of an integer is given by the product of all the integers that are equal or smaller than it. For example, the factorial of 4 is:

`4!=1\cdot2\cdot3\cdot4`

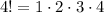
We must find the value of the following expression with factorials:

`(4!\cdot6!)/(2!\cdot5!)`

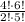
The first thing that we can do is expand the four factorials in the expression:

`(4!\cdot6!)/(2!\cdot5!)=(1\cdot2\cdot3\cdot4\cdot1\cdot2\cdot3\cdot4\cdot5\cdot6)/(1\cdot2\cdot1\cdot2\cdot3\cdot4\cdot5)`

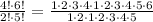
All the numbers on both the numerator and the denominator are multiplying. This means that if a number appears in the numerator and in the denominator it can be simplified. For example 1 appears twice in the numerator and twice in the denominator so it can be simplified:

`(1\cdot2\cdot3\cdot4\cdot1\cdot2\cdot3\cdot4\cdot5\cdot6)/(1\cdot2\cdot1\cdot2\cdot3\cdot4\cdot5)=(1\cdot1)/(1\cdot1)\cdot(2\cdot3\cdot4\cdot2\cdot3\cdot4\cdot5\cdot6)/(2\cdot2\cdot3\cdot4\cdot5)=(2\cdot3\cdot4\cdot2\cdot3\cdot4\cdot5\cdot6)/(2\cdot2\cdot3\cdot4\cdot5)`

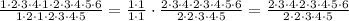
2 appears twice in both the numerator and the denominator so it can be simplified:

`(2\cdot3\cdot4\cdot2\cdot3\cdot4\cdot5\cdot6)/(2\cdot2\cdot3\cdot4\cdot5)=(3\cdot4\cdot3\cdot4\cdot5\cdot6)/(3\cdot4\cdot5)`

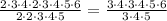
We have a 3, a 4 and a 5 in the denominator so we can simplify them with a 3, a 4 and a 5 of the numerator:

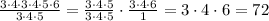
`(3\cdot4\cdot3\cdot4\cdot5\cdot6)/(3\cdot4\cdot5)=(3\cdot4\cdot5)/(3\cdot4\cdot5)\cdot(3\cdot4\cdot6)/(1)=3\cdot4\cdot6=72`Answer

Then the answer is 72.