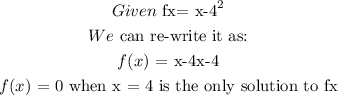
To graph f(x), we will notice that in vertex form the graph is:
f(x) = (x-4)^2 + 0
The vertex is therefore at (4;0). a =1, which means the parabola has a minimum at the vertex and is facing upwards.
The y intercept is found when x = 0
f(x) = (0-4)^2
f(x) = 16
The y intercept is at (0,16)
The below is therefore a graph of the function: