Question

In the spring of 2017, the Consumer Reports National Research Center conducted a survey of 1,007 adults to learn about their major healthcare concerns. The survey results showed that 579 of the respondents lack confidence they will be able to afford health insurance in the future. (a) What is the point estimate of the population proportion of adults who lack confidence they will be able to afford health insurance in the future. (Round your answer to two decimal places.) (b) At 90% confidence, what is the margin of error

Answer 1

a) The point estimate of the population proportion of adults who lack confidence they will be able to afford health insurance in the future us 0.58.

b) The margin of error is of 0.03.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
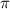`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

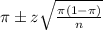
In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

Point estimate:

The point estimate is
`\pi`.

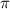Margin of error:

The margin of error is:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

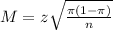
(a) What is the point estimate of the population proportion of adults who lack confidence they will be able to afford health insurance in the future.

579 out of 1007 adults. So

`\pi = (579)/(1007) = 0.575`

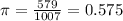
Rounding to two decimal places, 0.58

The point estimate of the population proportion of adults who lack confidence they will be able to afford health insurance in the future us 0.58.

(b) At 90% confidence, what is the margin of error

90% confidence level

So
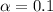`\alpha = 0.1`, z is the value of Z that has a pvalue of
`1 - (0.1)/(2) = 0.95`, so
`Z = 1.645`.

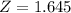The margin of error is:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`M = 1.645\sqrt{(0.58*0.42)/(1007)}`

`M = 0.03`

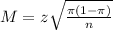
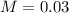
The margin of error is of 0.03.