A direct variation means that when one variable increase the other variable increases too, and when a variable decrease, the other variable decrease too. The increase and decrease follow a factor of variability, or slope.
To find the equation of a situation as given you need to find the slope and the y-intercept (the value of the function when the independient variable is 0)
Slope: You can use the next formula to find the slope in this situation:
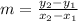
In the given table the first column is the independient variable (x) and the second column is the dependient variable (y).
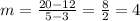
The slope of the given variation is m=4
Y-intercept: You use one row of data to find the y-intercept: (b)
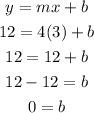
As the slope is m=4 and the y-intercept is b=0 you get the next equation:
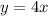
Then, the correct answer is yes, y = 4x