Given,
The length of the pipe, L=45.132 cm=0.45132 m
The speed of the sound is v=343 m/s
The frequency of the 1 st harmonic is given by,
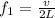
On substituting the known values,
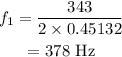
The frequency of the second harmonic is given by,
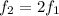
On substituting the known values,
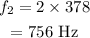
The frequency of the third harmonic is given by,
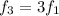
On substituting the known values,
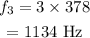
Therefore the frequency of 1st harmonic is 378 Hz.
The frequency of the 2nd harmonic is 765 Hz
The frequency of the 3rd harmonic is 1134 Hz