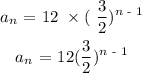ANSWER
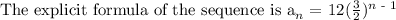
Explanation:
Given the below sequence
12, 18, 27, 40.5, 60.75
From the sequence provided, you will see that the sequence is a geometric sequence
The next step is to find the common ratio

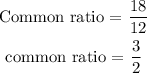
Recall that, the nth term of a geometric progression is given as
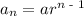
Where
a = first term
n = number of terms
r = common ratio
The next thing is to find the explicit formula
From the given sequence, the first term of the sequence is 12, and the common ratio of the sequence is 3/2