Question

A skier is at rest on a hill sloped at 40° the coefficient of kinetic friction between the snow and the skis is 0.12 the skier starts skiing downhill how fast is the skier going after six seconds

Answer 1

The speed of the skier after six seconds is 35.2476 m/s.

Step-by-step explanation:

To find the speed of the skier after six seconds, we need to calculate the acceleration of the skier first. We can use the formula a = g*sin(theta) - uk*g*cos(theta), where g is the acceleration due to gravity (9.8 m/s^2), theta is the angle of the slope (40 degrees), and uk is the coefficient of kinetic friction (0.12).

Plugging in the given values, we have a = 9.8*sin(40) - 0.12*9.8*cos(40) = 5.8746 m/s^2.

Next, we use the formula v = u + a*t, where v is the final velocity, u is the initial velocity (0 m/s since the skier starts at rest), a is the acceleration, and t is the time (6 seconds).

Substituting the known values, v = 0 + 5.8746*6 = 35.2476 m/s.

Answer 2

We are given the following information

A skier is at rest on a hill sloped at 40°

The coefficient of kinetic friction between the snow and the skis is 0.12

How fast is the skier going after six seconds?

Let us first draw a free body diagram to better understand the problem

The sum of forces in the vertical direction is given by

`\begin{gathered} \sum F_y=0 \\ F_N-F_g\cos \theta=0 \\ F_N=F_g\cos \theta \end{gathered}`

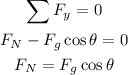
The sum of forces in the horizontal direction is given by

`\begin{gathered} \sum F_x=ma_x \\ F_g\sin \theta-F_k=ma_x \\ a_x=(F_g\sin\theta-F_k)/(m) \end{gathered}`

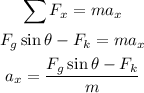
The force due to friction is equal to

`F_k=\mu_kF_N=\mu_kF_g\cos \theta`

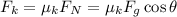
Where μk is the coefficient of kinetic friction between the snow and the ski.

`a_x=(F_g\sin\theta-\mu_kF_g\cos\theta)/(m)`

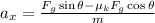
Substituting F = mg

`a_x=(mg\sin\theta-\mu_kmg\cos\theta)/(m)=(m(g\sin \theta-\mu_kg\cos \theta))/(m)`

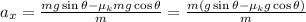
Mass cancels out

`\begin{gathered} a_x=g\sin \theta-\mu_kg\cos \theta \\ a_x=9.81\cdot\sin (40\degree)-0.12\cdot9.81\cdot\cos (40\degree) \\ a_x=6.3-0.9 \\ a_x=5.4\; \; (m)/(s^2) \end{gathered}`

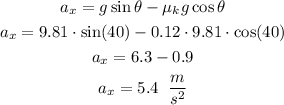
Finally, since we have acceleration, we can find the velocity using the following equation of motion

`v_f=v_i+a_x\cdot t`

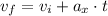
Where vf is the final velocity that we need to find out, vi is the initial velocity that is 0 since the skier was at rest initially and t is the time.

`\begin{gathered} v_f=0+5.4\cdot6 \\ v_f=32.4\; \; (m)/(s) \end{gathered}`

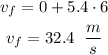
Therefore, the skier is going at 32.4 m/s